관계대수와 SQL
1. 관계 대수 vs SQL
-> SQL은 'what'을 이야기하고 '어떻게'를 처리하는 건 관계대수다.
-> SQL을 이용하여 관계 데이터베이스 릴레이션 정의, 정보 검색, 데베 갱신, 여러 무결성 제약조건 명시 가능
2. 관계 대수
- 기존의 릴레이션들로부터 새로운 릴레이션을 생성한다
- 릴레이션이나 관계 대수식에 연산자들을 적용하여 보다 복잡합 관계 대수식을 점차적으로 만들 수 있다
- 기본적인 연산자들의 집합으로 이루어졌다
- 단일 릴레이션이나 두개의 릴레이션을 입력으로 받아 하나의 결과 릴레이션 생성 (숫자=릴레이션, 산술연산자=관계연산자 느낌)
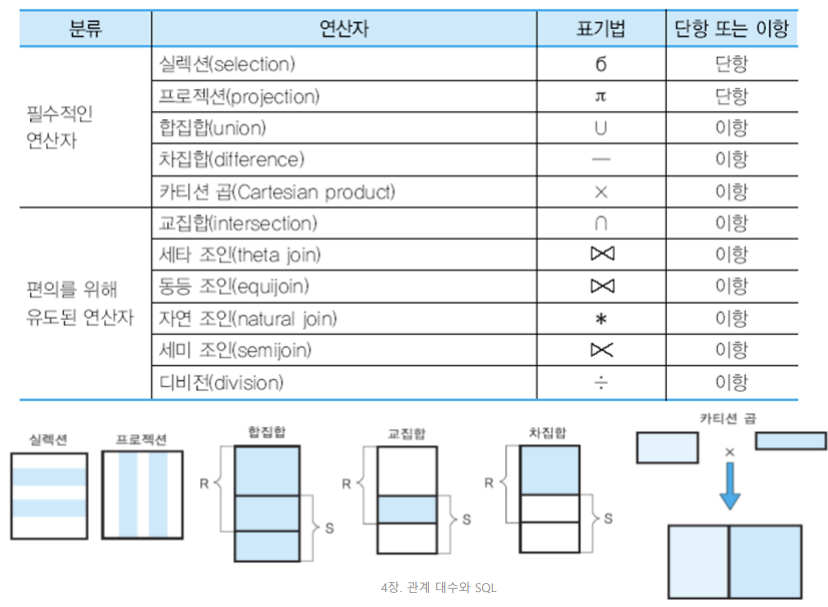
- 실렉션 : 조건식 만족하는 투플 반환
- 실렉션 조건= 프레디키트(predicate)
-> 릴레이션의 임의의 애트리뷰트와 상수, 비교 연산자, 부울 연산자(and, or, not)을 포함
- 결과 릴레이션에 중복 투플이 존재할 수 없음
- 프로젝션 : 릴레이션에서 애트리뷰트 리스트에 나열된 어트리뷰트 값으로만 구성된 투플 가져온다
- 한 릴레이션의 애트리뷰트들의 부분 집합을 구함
- 결과 릴레이션에 중복된 투플들이 존재할 수 있음. 따라서 중복을 제거해주어야 한다. cf) 애트리뷰트 리스트에 키가 포함되어 있으면 중복된 투플이 존재하지 않음
- -> 얘네 둘만 단항연산 (릴레이션 한 개에 적용된다)
- 집합 연산자
- 합집합, 교집합, 차집합연산자
- 이항 연산자이다
- 집합 연산자의 입력으로 사용되는 두 릴레이션은 합집합 호환 이어야한다.
-> 합집합 호한이란?
두 릴레이션의 애트리뷰트 수가 같고 각 애트리뷰트의 도메인이대응되는 attribute의 도메인과 같아야 한다.
-> 결국 attribute의 구조가 같아야 된다는 뜻
1) 합집합 연산자
-> 두 릴레이션 R, S에 대해 R or S에 있거나 R과 S 모두에 속한 투플들로 이루어진 릴레이션
-> 결과 릴레이션에서 중복된 투플들은 제외된다
-> 결과 릴레이션의 차수 = R or S의 차수
2) 교집합 연산자
-> R과 S 모두에속한 투플들로 이루어진 릴레이션
-> 결과 릴레이션의 차수는 R또는 S의 차수와 같다
3) 차집합 연산자
-> R-S ( R에는 속하지만 S에는 속하지 않은 투플들로 이루어진 릴레이션 )
->결과 릴레이션의 차수는 R또는 S의 차수와 같다
- 카티션 곱 연산자 -> 두개의 릴레이션을 결합시킬 때 사용된다
-> R*S
-> 차수가 n+m ( R의 차수가 n, S의 차수가 m )
-> 카디날리티 i*j
-> 애트리뷰트 :(A1, A2, ..., An, B1, B2, ..., Bm)
-> R과 S의 투플들의 모든 가능한 조합으로 이루어진 릴레이션
-> 결과 릴레이션의 크기가 매우 클 수 있으며 사용자가 원하는 건 일부인 경우가 대부분이라 카티션 곱이 유용한 연산자 는 아님
- 조인 연산자
- 두 개의 릴레이션으로부터 연관된 투플들을 결합하는 연산 ( 두 개 이상의 릴레이션들의 관계를 다룬다 )
- 세타조인, 동등 조인, 자연 조인, 외부 조인, 세미 조인 등
1) 세타 조인과 동등 조인
- 조인 조건을 만족하는 투플들로 이루어진 릴레이션 ( 조건 만족하는 투플들만 결합시켜 준다) ( 모든 경우의 투플들이 오는 건 아니다)
- 세타 조인 -> { =, <>, <=, <, >=, > } 중 하나
- 동등조인 -> 세타 조인 중 비교 연산자가 =인 조인
2) 자연 조인
- 동등 조인의 결과 릴레이션에서 조인 애트리뷰트를 한 개 제외한 조인
- 똑같은 값이 두 개가 왔을때 하나만 나타냄
3) 디비전 연산자 (나누기 연산자)
- R/S
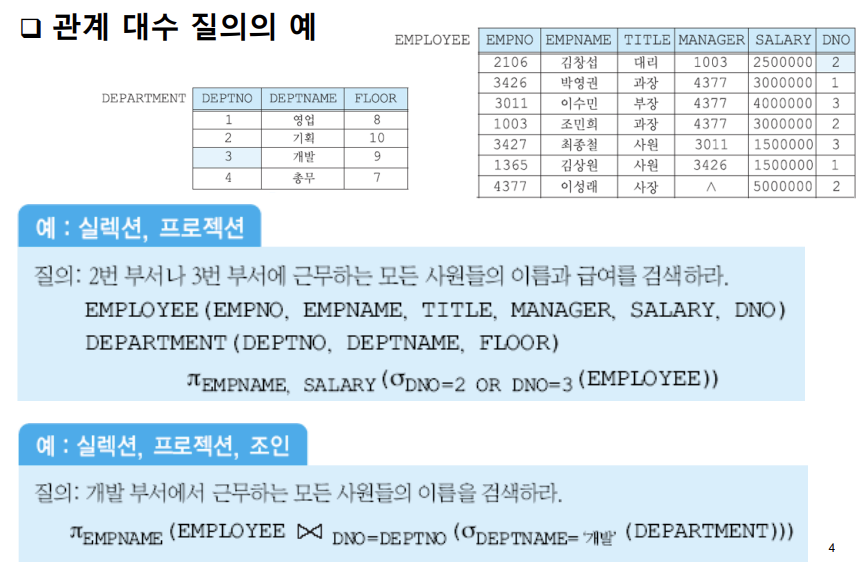
- 차수가 m인 릴레이션 S에속하는 모든 투플 u에 대하여 투플 tu (투플 t와 u를 결합한 것) 가 차수가 m+n인 릴레이션 R에 존재하는 투플 t의 집합 ( R의 투플 중 S에 속하는 모든 투플을 담고 있는 투플들만 골라 추출 )
-> 피피티 예시 그림 참고하기
- 관계 대수의 한계
-> 관계 대수는 산술 연산을 할수 없음
-> 집단 함수를 지원하지 않음
-> 정렬 나타낼 수 없음
-> 데이터베이스 수정 불가
-> 중복된 투플을 나타내는 것이 필요할 때가 있는데 이를 명시하지 못함