Unsupervised learning : label이 주어지지 않음! (y값)
-> unlabeld data의 structure를 학습하는 방식으로 이루어진다
ex) clustering, dimensionality reduction
Clustering
-> simmilar object들을 같은 cluster로 묶는 기법
-> 그렇다면 "simmilar object"인지 어떻게 결정할까?
1) Centroid-based clustering
: centroid = cluster의 center
: data가 centroid로부터 얼마나 떨어졌는지 계산한다
: ex) K-means

2) Density-based clustering
: high density 영역을 연결한다
: ex) DBSCAN
3) Distribution-based clustering
: data가 특정 distribution에 있다고 가정한다
: data를 pre-defined distribution에 cluster한다
: ex) Gaussian mixture model

4) Hierarchical clustering
: tree of cluster를 만든다
: 하나의 cluster가 나타날 때까지 bottom-up joining 을 한다

Clustering algorithm
-> K-nn
-> Hierarchial clustering
-> DBSCAN
-> Gaussian mixture model
K-means
K : cluster 개수
step 1) k개의 data point를 랜덤으로 고른다
step 2) 각 data point와 centroid 사이의 거리를 계산한 후 어느 centroid와 가장 가까운지 판단한다
(거리 계산 방법 : Euclidean distance / Manhattan distance
simmilarity metric : cosine similarity)
step 3) initial 위치로부터 실제 cluster의 중심이 되도록 centroid 재설정
-> 더이상 centroid 위치에 변화가 없을 때까지 1~3 반복

-> initial centroid에 따라 최종 cluster가 달라진다
-> K는 어떻게 정할까?!
: 형성된 cluster 안의 variance가 작을수록 좋다(centroid 위치가 많이 바뀌는지)
K-means의 단점
: initial centroid와 outlier에 clustering결과가 예민하다. 따라서 파라미터로 효과적인 cluster 개수를 결정하는 게 중요하다
Hierarchial clustering
: 처음에 각 data point를 single cluster로 보고 시작하여 가장 가까운 cluster끼리 묶는다.
-> 하나의 cluster가 될때까지 묶는다

"similarity" 계산하는 방법
1) Single linkage : cluster 간의 가장 짧은 거리 계산

2) Complete linkage : cluster 간의 가장 먼 거리 계산

3) Average linkage : 두 cluster 간에 pair-wise 거리 계산

4) Centroid linkage : centroid 간의 거리 계산

Cluster 정하는 방법
Dendrogram

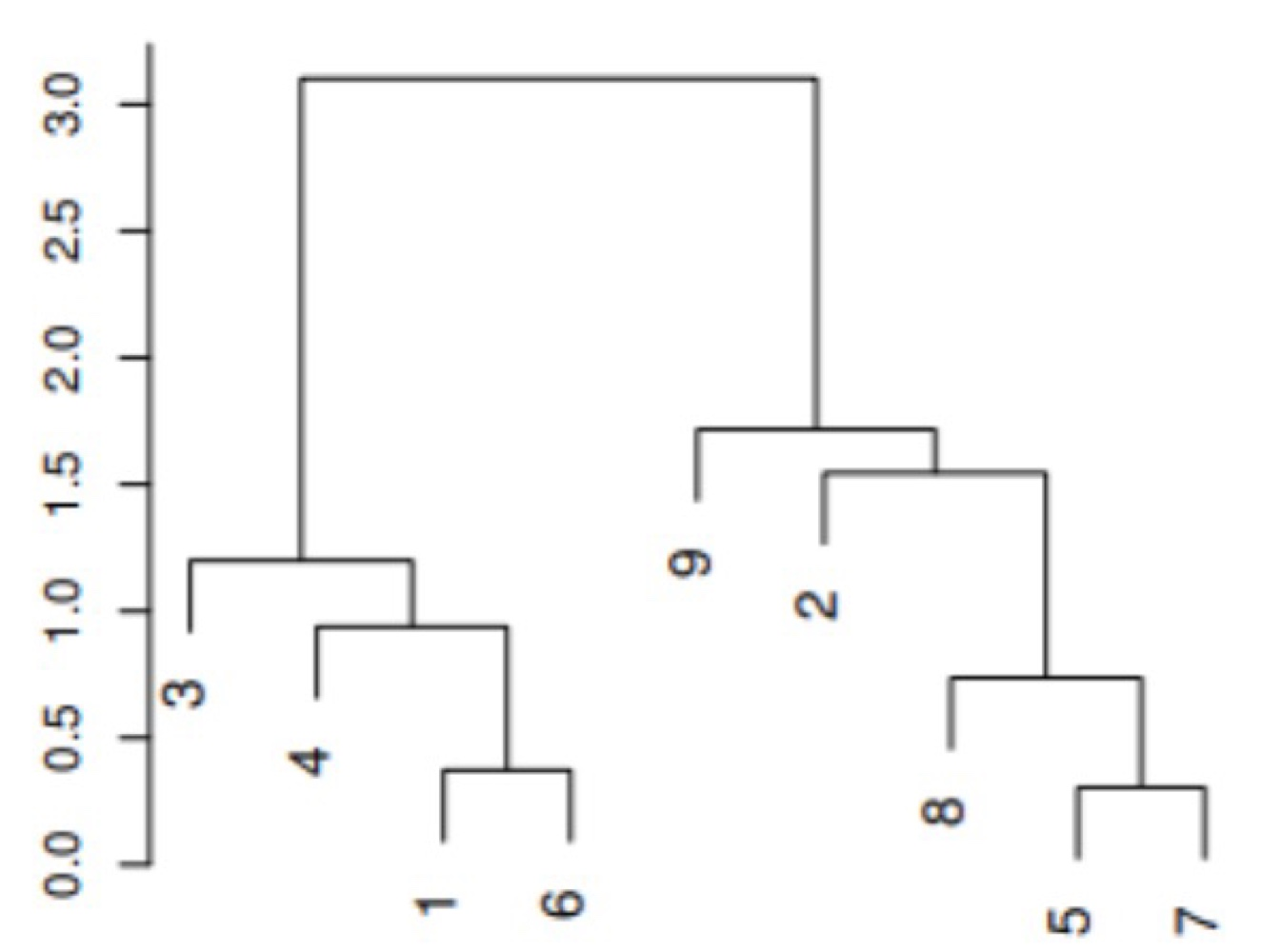
Height = data point들이 얼마나 dissimilar한지 나타낸다
data들끼리 더 빨리 merge 될수록 더 similar 하다는 뜻이다. (9는 8보다 2와 simmilar하다)
K-means와 Hierarchial clustering의 cluster 정하는 방법 차이점
-> K-means는 미리 k의 개수를 정해야 하기에 부담스럽다
-> Hierarchial clustering은 다양한 k 개수로 explore 해볼 수 있다
Gaussian mixture model (GMM)

: 전제 조건 -> data가 gaussian distribution 따른다
: multiple Gaussian distribution이 mixture 된 것
: mixing coefficient를 사용한다
-> mixing coefficient란? : 각 gaussian model이 x에 미치는 영향의 정도를 알기 위해 사용
: Evaluation step & Maximization step으로 이루어짐
1) Evaluation step : 각 data point들이 각 gaussian distribution에 속할 확률을 계산하고 가장 likelihood가 높은 거에 할당
2) Maximization step : iterative하게 각 gaussian distribution의 mean과 variance를 업데이트 시킴
-> GMM은 EM algorithm이라고 불린다
-> Log liklihood를 사용하여 liklihood 계산하는 E 단계 / 이 예측을 최대화시키는 각 분포의 평균, 분산을 추정하는 M 단계
이제 다시 원래 설명하려했던 GMM으로 넘어오자.
k개의 gaussian distribution mixture에 data가 있다고 가정하자 (k는 pre-defined 된 값)
목표 : 주어진 data에 잘 들어맞는 Gaussian distribution의 mixture 찾는 것 -> log likelihood 이용하기
1) p(xi) 구하기
2) optimization : x의 log liklihood를 maximize하여 k gaussian distribution에 x가 나타날 확률을 최대화 함
3) zi는 알려지지않았기에 추정해야함. 이때 EM algorithm 사용하기

공식 외우기!!
DBSCAN
: Density-based clustering
: Distance뿐만 아니라 connectivity에도 집중한다

cf) K-means 는 data point가 curvy 하면 제대로 동작하기 힘듦

: Core points -> main driver(clustering에 영향 끼치는 애들)
: Border points -> corepoint의 neighbor이지만 충분한 neighbor를 갖고 있지 않는 애들
: Noise -> 어느 cluster에도 할당되지 않는다
: MinPts -> cluster의 neighbor 개수 (Core point인지 결정하는 요소)
: Eps -> 이웃인지 아닌지 결정하게 되는 요소
: DBSCAN algorithm의 파라미터 : eps / MinPts / distance metrics
step 1)
eps 이용해서 neighbor 찾고, MinPts 이용해서 corepoint인지 border point인지 noise인지 찾기
-> distance(x,z)<=eps :neighbor of x
-> x의 neighbor개수 >= MinPts-1 : core point
-> x의 neighbor개수 < MinPts-1 & core point의 neighbor : border point
-> x의 neighbor개수 < MinPts-1 : noise
step 2)
core point x를 중심으로 하는 cluster 만들기. x에 속하는 이웃 중 다른 cluster의 core point가 된다면 두 cluster는 같은 cluster로 바라보기
step3)
모든 dataset에 대해 반복. 아무 cluster에도 속하지 않으면 noise다
장단점

'인공지능 > Machine Learning' 카테고리의 다른 글
| K-nn (0) | 2023.12.13 |
|---|---|
| Unsupervised learning - PCA (0) | 2023.12.13 |
| model assessment (0) | 2023.12.11 |
| Decision tree (0) | 2023.10.26 |
| Soft margin classifier (0) | 2023.10.25 |



