배경지식을 짚고 넘어가자!
- eigenvector : 방향은 변하지 않고 크기만 변하는 벡터들
- eigenvalue : 얼마만큼 크기가 변했냐
그렇다면 왜 차원 축소(dimensionality reduction)가 필요할까?!
1) 차원의 저주 (curse of dimensionality)
: 데이터 차원이 커진다면 data가 sparse 해져 모델이 data를 이해하는 데 방해 된다. 따라서 data가 sparse해진다면 model의 complexity가 증가하게 된다
2) multicollinearity
: 데이터 차원이 커진다면 상관관계 갖는 feature들이 생길 확률이 증가한다
-> 이렇게 data 차원이 커지면 문제가 생기므로 많은 feature가 주어졌다면 아래와 같은 것들을 하는 게 중요하다
1) Feature selection
: 상대적으로 덜 중요한 feature들은 ignore하자
2) Feature extraction
: 차원이 낮은 축에 투영시켜 차원을 줄인다 (ex)PCA)
: 하나의 dimension을 제거하면(remove one dimension) data가 overlap 될 수 있기에 문제다
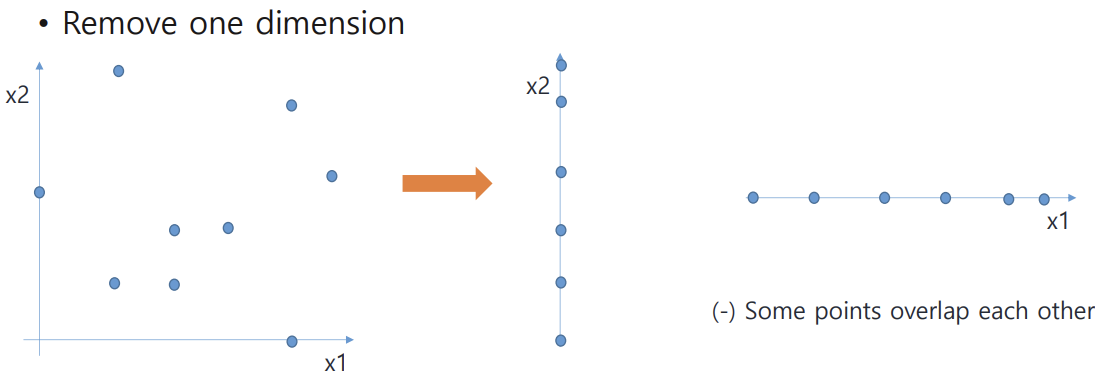
: 새로운 축(new dimension) 찾고 여기에 data들을 투영시키는 게 좋은 방법!!

3) Feature engineering
: data에 대한 전문적인 도메인 지식에 기반한 feature들을 계산해 사용한다
PCA (Principal Component Analysis)
: 고차원의 데이터를 낮은 차원의 데이터로 바꿔준다 (feature extraction techniques)
: label을 필요로 하지 않는다 (unsuperviesd)

이때 새로운 축을 찾는 기준 (principal conmponent)
-> data를 투영시켰을 때 data들끼리 겹쳐지기보다 최대한 떨어져 있는 게 좋다!!! (high variance 만드는 축 찾기)
-> candidate축을 360도 회전시켰을 때 variance를 가장 크게 만드는 축 찾는 게 PCA의 목표다!!! 이 축이 principal component를 의미한다

그렇다면 이러한 axis를 어떻게 찾을까?!
1) normalize data (평균 1, 표준편차 1)
-> normalization 하는 이유 : 새로 투영된 점이 origin으로 부터 거리가 얼마나 떨어졌는지 알기 위해
2) 투영된 data들의 variance가 maximize되는 unit vector u 찾기 (데이터에서 원점을 지나는 직선에 수선의 발을 내려
해당 점과 원점 사이의 거리가 최대가 되는 직선 찾기)
찾은 후 이 길이 제곱들의 합이 최대가 직선을 찾는다 -> 이렇게 찾아진 게 principal component가 된다


D라는dimension을 k라는 차원으로 축소 = unit vector k개를 찾는 것
unit vector u(우리가 찾으려는 새로운 축, 즉 principal component)들은 서로 orthogonal 해야함 (feature들이 uncorrelated되기 위해)

-> zi : 새로운 k라는 차원으로 차원축소된 space에 투영된 점들
<정리>
u=principal component
eigen value=variance
PCA step
step 1) Normalize given data points
step 2) covariance matrix 계산하기
step 3) eigen value & eigen vector 계산하기
step 4) eigen vector = principal component / eigen value = eigen vector에 투영된 점들의 variance 된다
'인공지능 > Machine Learning' 카테고리의 다른 글
| K-nn (0) | 2023.12.13 |
|---|---|
| Unsupervised - Clustering (0) | 2023.12.12 |
| model assessment (0) | 2023.12.11 |
| Decision tree (0) | 2023.10.26 |
| Soft margin classifier (0) | 2023.10.25 |



