K-nn 이란?
- test data z가 주어지면 training data 중 가장 가까운 거리 or 가장 유사도 큰 k개의 training data를 찾고, 이 k개의 neighbor에서 majority vote를 통해 z의 label 정하는 방식
- supervised learning (정답값, 즉 label이 주어짐)
- train 과정이 필요 없다
- Memory-based learning (training data points들을 외워서 test data와의 거리 / 유사도 파악해야해서)
- Cheap training & Expensive testing
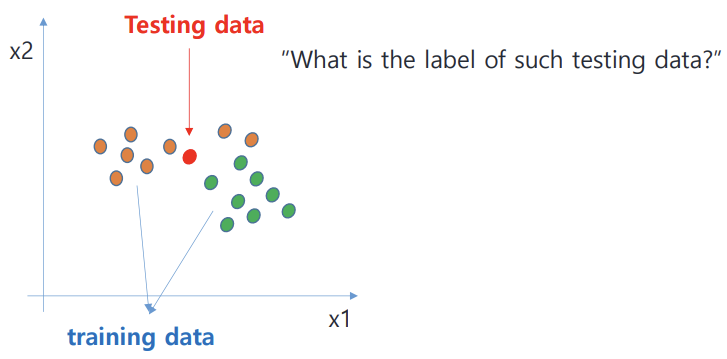
그렇다면 similarity나 closeness를 어떤 방식으로 판단할까?!
1) Distance-based metrics
- Euclidean distance : (L2 distance. 제곱), 가장 흔히 사용됨

- Manhattan distance : (L1 distance)

- Minkowski distance : 일반화된 형태 (Lp distance)
: 차원이 아무리 많아도 각 axis에서 L1 distance구하고 그 중 가장 큰 값 취함
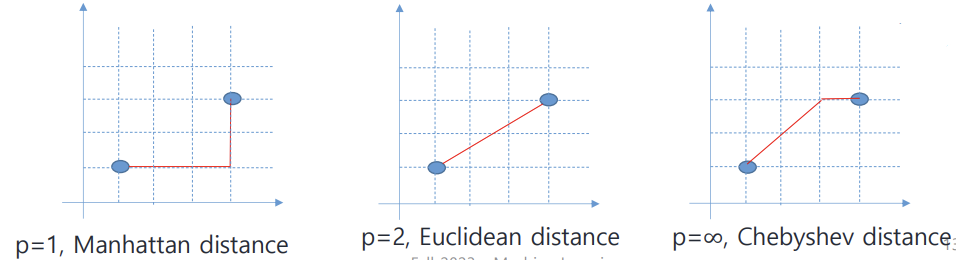
Chebyshev distance
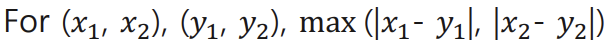

2) Simmilarity-based metrics
- Cosine distance : 두 벡터 사이의 cosine angle 이용해 유사도 측정
: 두 벡터가 같은 방향일수록 simmilarity 증가 (-1<simmilarity<1)
: 즉, 두 벡터가 이루는 각의 크기가 작을수록 simmilarity 증가
- Jaccard distance : NLP에서 가장 많이 사용되는방식
: (공통 단어 수) / (총 단어수 로 유사도 계산)

3) Hamming distance : NLP에서 가장 많이 사용되는 방식
: 두 binary string의 길이가 같을 때 사용!
: 유사도 = (같은 자리에 같은 문자 있는 갯수) / (총 string의 길이)
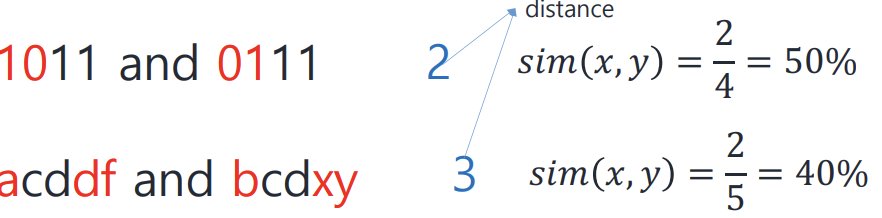
Decision boundary with K-nn
k-NN does NOT explicitly compute the decision boundary rather, it can be inferred.
K-nn algorithm
1) standardize the features (평균 0, 표준편차 1로)
-> k-nn은 distance based이기에 scale이 크다는 이유만으로 그거에 해당하는 feature가 distance에 큰 영향 줄 수 있다. 따라서 두 feature의 scale이 너무 다르면 문제가 되기에 normalize 한다
2) testing instance와 가장 가까운 k개의 training sample 찾기
3) majority class로 test data의 label 결정하기
K에 대하여...
K 증가 -> classifier가 oulier에 덜 sensitive하다는 뜻
: outlier가 섞여 있어도 label이 확확 바뀌지 않는다는 뜻
따라서 larger K -> better performance로 이끈다
but K가 너무 크면, neighbor가 아니더라도 neighbor로 detect하게 되는 문제
good K를 찾기 위해서는 cross-validation을 이용해야 한다
recommended : k < 루트n (n=training sample 총 갯수)
K-nn의 단점
- expensive testing time
:모든 training sample과 test sample의 distance를 계산해서 최근접한 이웃 K개를 뽑아야 하기에 거리를 다 계산해야 해서
- high storage requirement
: 모든 training sample 저장하고 있어야 한다 (매 test sample을 evaluate 할때마다 그 거리 계산해야해서)
'인공지능 > Machine Learning' 카테고리의 다른 글
| Unsupervised learning - PCA (0) | 2023.12.13 |
|---|---|
| Unsupervised - Clustering (0) | 2023.12.12 |
| model assessment (0) | 2023.12.11 |
| Decision tree (0) | 2023.10.26 |
| Soft margin classifier (0) | 2023.10.25 |



